The Weekly Challenge ‐ Perl and Raku

CY's Take on The Weekly Challenge #123 ‐ N-cube

If you want to challenge yourself on programming, especially on Perl and/or Raku, go to https://theweeklychallenge.org, code the latest challenges, submit codes on-time (by GitHub or email).

Do tell me, if I am wrong or you strongly oppose my statements!

It's time for challenges in Week #123 !

about 1500 words, so a brief content:

Prelude

I often wrote my blogpost for TWC in a storytelling style, but I feel that its my time to put it more "coding-ly" as my knowledge on programming increases. Arrrrrrr... Sometimes I have shared my offline life in these blogposts, I decide to put it in the bottom of the blogpost if it wants.

image info

As noted in the Wikipedia, the generation of ugly numbers is "often used to demonstrate the power of a lazy functional programming language", and I haven't known what functional programming is (find some interesting resources like here or here recently, however I guess, for me, it is better to learn Haskell, a purely functional programming language, /*with Category theory in math, */ in order to grasp the idea of FP throughfully; I need discipline to learn skills OR I WILL STRAY TOO FAR LIKE FOR TASK TWO THIS WEEK).

I have used brute-force ideas to solve the task one. Not nice to share.

Task 2: Square Points

Oh, I like the task too much and decide for me to unusually quote the original task statements here:

TASK #2 › Square Points
Submitted by: Mohammad S Anwar

You are given coordinates of four points i.e. (x1, y1), (x2, y2), (x3, y3) and (x4, y4).

Write a script to find out if the given four points form a square.

After seeing the task statements I immediately decided to extend it as a square+cube+hypercube task in arbitary dimensions!

Math Fun: On the Geometry of 3D and 4D space

Hey, do allow me introduce two cool terms I recently learnt: "ana" and "kata". In an Euclidean 3D space, which most of us believe ourselves are familiar with, we can have Up/Down/North/East/South/West (or Up/Down/Back/Left/Front/Right, esp. if you have played Rubik's Cube). In 4D, there is one more axis, thus two more directions we can have, and some mathematicians assign "ana" and "kata" as the names for those directions.

[Need not to fancy too much about "time as the fourth dimension"... The "metric" for measuring distance used by physicists for the dimension of time is called Minkowski metric (generalized: Lorentzian metric). And that "4D world" is called Minkowski spacetime.]

In my submitted codes, A/K/U/D/N/E/S/W are used; the South-East-Down point is picked to be the initial point for vector calculation in 3D and the Kata-South-East-Down point is picked for the same purpose in 4D.

Properties of Squares (and Cubes) and a Primitive Algorithm

A quadrilateral with 4 sides equal can be a rhombus but not a square.

A polyhedron with its 12 sides equal can be a parallelepiped but not a cube.

To conclude, we have to get more details besides calculations of the lengths of edges.

Before jumping to the next section about cube-check and hypercube-check, we may have to consider checking for the square first.

Let a be the length of an edge of the regular "cube-like" polytope.

Though edges are not sufficient conditions for proving/disproving whether a polytope(the umbrella term for polygon, polyhedron, ...) is a "cube-like" polytope, it seems that we must know their lengths and check whether they are equal. All we have on hand is the coordinates of vertices, without given their "order" in the plane/space.

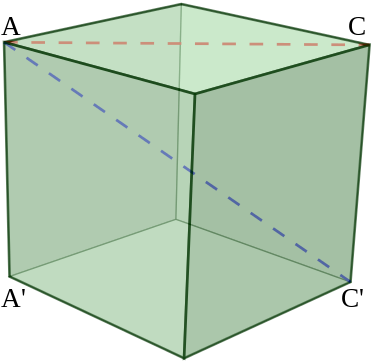
Discuss the case of a square. We name the vertices are p0, p1, p2, and p3. We have the segment between pm and pn can be either an edge or a diagonal. We have 6 segments to consider. And we know from high school math that sqrt(2)*a is the length of the diagonal.

As mentioned, an edge-equal quadrilaternal can be a rhombus. But if we additionally consider the length of diagonals, the square has equal-length diagonals and an arbitarily constructed rhombus usually does not. Hence we can have a simple algorithm:

say is_square($pt0, $pt1, $pt2, $pt3);


sub is_square {
    my ($p0,$p1,$p2,$p3) = ($_[0], $_[1], $_[2], $_[3]);

    my @n_vector = map { norm($_) } ($v0, $v1, $v2, ... );
    @n_vector = sort {$a<=>$b} @n_vector;

sub norm {
    my $p = $_[0];
    my $sum = 0;
    $sum+= ($p->[$_])**2 for (0..$p->$#*);
    return $sum;
}

ok is_square( [10,20], [20,20], [20, 10], [10, 10] ) == 1, "Example 1";
ok is_square( [12,24], [16,10], [20, 12], [18, 16] ) == 0, "Example 2";
ok is_square( [1, 2] , [4,3], [3,1], [2,4] ) == 1, "Knight's square";
ok is_square( [1, 1] , [-1, 1], [ 1,-1], [-1,-1] ) == 1, "centre at origin";

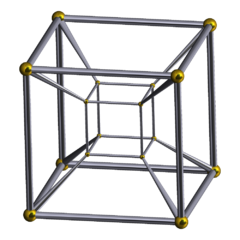
Math Fun: Properties of n-hypercube

image info

Shouldn't we investigate some basic stuff about the cube in order to understand the hypercube?

Cube:
Number of vertices: 8
Number of edges: 12
Number of faces: 6
Number of cubes: 1

Especially for the segments between pairs of vertices:
Number of edges: 12
Number of face diagonals: 12
Number of body diagonals: 4
Total Number of Segments: 28

Calculate again for the properties of a cube from those of a square:
Cube:
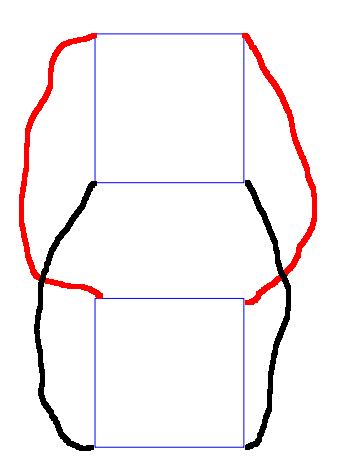
Number of vertices: num of vertices in a square × 2 = 4 × 2 = 8
Number of edges: num of edges in a square × 2 + 4 edges from the self replicating process (black and red in the diagram) = 4 × 2 + 4 = 12
Number of faces: 6
Number of cubes: 1

See a supporting diagram.

Look at the diagram of the hypercube on right in order to get some sensation on it.

image info

Now we proceed (can be counted from looking at the diagram):
Hypercube:
Number of vertices: 8 × 2 = 16
Number of edges: num of edges in a cube × 2 + 8 edges from the self replicating process = 12×2 + 8 = 32
Number of faces: num of faces in a cube × 2 + 12 faces new = 6×2 + 4×6÷2 = 24
Number of cubes: 2 + 6 = 8

Especially for the segments between pairs of vertices:
Number of edges: 32
Number of face diagonals: 2×24 = 48
Number of body diagonals: 4×8 = 32
Number of "hyperdiagonals": 8
Total Number of Segments: 120

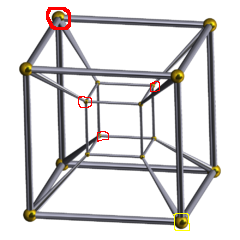
I have circled the four body-diagonal points with respect to the bigger bottom right point in red colour as I think it might be the most difficult for us to catch them by intuition.

Though we are not going to code for the 5-hypercube, we may try some calculations based on above.

5-hypercube. Yup, disclamier: I cannot "sense" how the 5-hypercube looks like. Here are just calculations (number of edges verified on OEIS sequence A001787) :
Number of vertices: 32
Number of edges: 32×2 + 16 = 80
Number of faces: 20×2 + ? × ? ÷ ? = ??

Oh, I resign, I fail to continue to count the remaining! But we can see there are already 80 edges, we can expect an order of magnitude of 10² or above for the totol number of concerned segments in 5-hypercube.

Vector Sum Approach

As said, we cannot solely rely on the length of edges. And the section "Properties of Squares (and Cubes) and a Primitive Algorithm" has already provided an algorithm and codes, what am I going to talk about?

If you read the optional section "Properties of n-hypercube", you will find there would be a huge number of length of segments we are going to calculate if we follow the primitive algorithm.

Another side of the primitive algorithm we need to consider is: are there any polytope with same various diagonals which are the same? Intuitively the answer is yes, but... I haven't proved it. So it remains a "conjecture" in our context. So... I don't think it is a safe approach for extending to cube or hypercube. A safer approach under the condition that "the diagonal conjecture is not yet proved" is checking the norm of a diagonal against the norm of an edge.

OK let us see the code now:

sub is_square {
    my ($p0,$p1,$p2,$p3) = ($_[0], $_[1], $_[2], $_[3]);
    my $v0 = vec_subtract($p0, $p1);
    my $v1 = vec_subtract($p0, $p2);
    my $v2 = vec_subtract($p0, $p3);
    # "dot product test";
    # return 0 unless (vec_prod_f($v1, $v2) == 0) xor
    #                (vec_prod_f($v0, $v2) == 0) xor
    #                (vec_prod_f($v0, $v1) == 0);
    my @n_vector = map { norm($_) } ($v0, $v1, $v2);
    @n_vector = sort {$a<=>$b} @n_vector;
    # "norm test"
    #if ( $n_vector[0] == $n_vector[1] ) {
#   the above conditional is fit for integter coordinates
#   the below is special arrangement starting from the 5th test case 
#   or floating point number in general
    if ( sprintf("%f",$n_vector[0]) == sprintf("%f", $n_vector[1])
       && 2*sprintf("%f", $n_vector[0]) == sprintf("%f", $n_vector[2])
#       the above line concerning length of diagonal is sqrt(2)
#       times the edge length would not be a necessary check 
#       if we preserve the dot product test, because in
#       Euclidean space, if two vectors are orthogonal and in equal length,
#       we can apply the Pythagorean theorem for the norm of the vector sum.
#       For DEMOSTRATION PURPOSE, 
#       the test of orthogonality (the dot product test) is commented out by brace,
#       but the dot product test will be used both for cube and hypercube.
         ) {
        return 1;
    }
    return 0;
}

sub vec_prod {
    my $first = $_[0];
    my $second = $_[1];
    warn "Not the same dimension in vec_prod \n" if $first->$#* != $second->$#*;
    my $sum = 0;
    $sum+= ($first->[$_]*$second->[$_]) for (0..$first->$#*);
    return $sum;
}

sub vec_subtract {
    my $first = $_[0];
    my $second = $_[1];
    my $ans = [];
    warn "Not the same dimension in vec_subtract\n" if $first->$#* != $second->$#*;
    for my $s (0..$first->$#*) {
        push $ans->@*, $second->[$s] - $first->[$s];
    }
    return $ans;
}

By the properties of vectors, the diagonal vector is the vector sum of two vectors representing the edge while we are keeping the direction correctly.

I will discuss the ugly &sprintf() (gonna be replaced by &norm_f ) on the later section "Numerical Inaccuracy". See also the reason of not using dot product test; honestly I am not sure which (dot product test or checking the norms) is a better combat against numerical inaccuracy; therefore they are being "comment out" via =pod.

Adventure to Cube and Hypercube

I intentionally avoid using permutations in the &is_cube here but using permtutations in &is_hypercube for DEMOSTRATING the logic more explicitly for some potential audience. Three nested conditionals, acceptable (?). You can get the link for finalized, more concise code at the bottom of the page.

sub is_cube {
    my @p = @_;
    my %v;
    $v{$_} = vec_subtract($p[0], $p[$_]) for (1..7);
    my @ind = sort { norm($v{$a}) <=> norm($v{$b}) } keys %v;
    my ($N, $W, $U) = ($v{$ind[0]} , $v{$ind[1]} , $v{$ind[2]}) ;
    return 0 unless norm_f($N) == norm_f($W) && norm_f($N) == norm_f($U);
    return 0 unless vec_prod_f($N,$W) == 0 && vec_prod_f($W,$U) == 0
                        && vec_prod_f($U,$N) == 0;
    my $NW = vec_sum($N, $W);
    my $WU = vec_sum($W, $U);
    my $UN = vec_sum($U, $N);
    my $bool = undef;
    if (vec_same_f($NW, $v{$ind[3]})) {
      if   (  vec_same_f($WU, $v{$ind[4]})
          &&  vec_same_f($UN, $v{$ind[5]}) ) { $bool = 1;
      } elsif ( vec_same_f($WU, $v{$ind[5]})
           &&   vec_same_f($UN, $v{$ind[4]}) ) { $bool = 1;
      }
    }
    if (!$bool && vec_same_f($NW, $v{$ind[4]})) {
      if   (  vec_same_f($WU, $v{$ind[3]})
          &&  vec_same_f($UN, $v{$ind[5]}) ) { $bool = 1;
      } elsif ( vec_same_f($WU, $v{$ind[5]})
           &&   vec_same_f($UN, $v{$ind[3]}) ) { $bool = 1;
      }
    }
    if (!$bool && vec_same_f($NW, $v{$ind[5]})) {
      if   (  vec_same_f($WU, $v{$ind[4]})
          &&  vec_same_f($UN, $v{$ind[3]}) ) { $bool = 1;
      } elsif ( vec_same_f($WU, $v{$ind[3]})
           &&   vec_same_f($UN, $v{$ind[4]}) ) { $bool = 1;
      } else {
        return 0;
      }
    }
    return 0 if !$bool;

    my $NWU = vec_sum( $N, $WU);
    if ( vec_same_f( $v{$ind[6]} , $NWU ) ) {
=pod
        return 0 unless
            2*norm_f($N) == norm_f($NW) &&
            norm_f($NW) == norm_f($WU) &&
            norm_f($WU) == norm_f($UN) &&
            3*norm_f($N) == norm_f($NWU);
=cut
        return 1;
    }
    else {
        return 0;
    }
}

sub is_hypercube {
    my @p = @_;
    my %v;
    $v{$_} = vec_subtract($p[0], $p[$_]) for (1..15);
    my @ind = sort { norm($v{$a}) <=> norm($v{$b}) } keys %v;
    my ($N, $W, $U, $A) = ( $v{$ind[0]}, $v{$ind[1]} ,
                            $v{$ind[2]}, $v{$ind[3]} );
    return 0 unless
        norm_f($N) == norm_f($W) && norm_f($W) == norm_f($U)
                             && norm_f($U) == norm_f($A);
    return 0 unless
        vec_prod_f($N, $W) == 0 &&
        vec_prod_f($N, $U) == 0 &&
        vec_prod_f($N, $A) == 0 &&
        vec_prod_f($A, $W) == 0 &&
        vec_prod_f($A, $U) == 0 &&
        vec_prod_f($W, $U) == 0 ;

    my $AU = vec_sum($A, $U);
    my $AW = vec_sum($A, $W);
    my $AN = vec_sum($A, $N);
    my $NW = vec_sum($N, $W);
    my $WU = vec_sum($W, $U);
    my $UN = vec_sum($U, $N);
    my $bool_face = undef;
    my $iter_face = permutations([$AU, $UN, $NW, $WU, $AW, $AN]);
    while (!$bool_face && (my $p = $iter_face->next)) {
        $bool_face =
            vec_same_f($v{$ind[4]}, $p->[0]) &&
            vec_same_f($v{$ind[5]}, $p->[1]) &&
            vec_same_f($v{$ind[6]}, $p->[2]) &&
            vec_same_f($v{$ind[7]}, $p->[3]) &&
            vec_same_f($v{$ind[8]}, $p->[4]) &&
            vec_same_f($v{$ind[9]}, $p->[5]) ;
    }
    return 0 if !$bool_face;

    my $UNW = vec_sum($UN, $W);
    my $ANW = vec_sum($NW, $A);
    my $AWU = vec_sum($WU, $A);
    my $AUN = vec_sum($UN, $A);
    my $bool_cube = undef;
    my $iter_cube = permutations([$UNW, $ANW, $AWU, $AUN]);
    while (!$bool_cube && (my $p = $iter_cube->next)) {
        $bool_cube =
            vec_same_f($v{$ind[10]}, $p->[0]) &&
            vec_same_f($v{$ind[11]}, $p->[1]) &&
            vec_same_f($v{$ind[12]}, $p->[2]) &&
            vec_same_f($v{$ind[13]}, $p->[3]);
    }
    return 0 if !$bool_cube;

    my $AUNW = vec_sum($AU,$NW);
    if ( vec_same_f($v{$ind[14]}, $AUNW) ) {

=pod
        return 0 unless 
            2*norm_f($N) == norm_f($NW) &&
            norm_f($NW) == norm_f($AU) &&
            norm_f($NW) == norm_f($UN) &&
            norm_f($NW) == norm_f($WU) &&
            norm_f($NW) == norm_f($AW) &&
            norm_f($NW) == norm_f($AN) &&
            3*norm_f($N) == norm_f($UNW) &&
            3*norm_f($N) == norm_f($ANW) &&
            3*norm_f($N) == norm_f($AWU) &&
            3*norm_f($N) == norm_f($AUN) &&
            4*norm_f($N) == norm_f($AUNW);
=cut
        return 1;
    }
    else {
        return 0;
    }
}

Numerical Inaccuracy

When all the coordinates are integers, there will not be any problems. What if we supply sqrt($INT) or sin($ANGLE)? It was found that Perl 5 (maybe many other programming language which are not built-in radical or "good sin function"). does not work well. Luckily a rouadabout is found:
sprintf("%f", $non-integer-value).

Here are code excepts from ch-2-cube-hypercube.pl:

sub vec_prod {
    my $first = $_[0];
    my $second = $_[1];
    warn "Not the same dimension in vec_prod \n" if $first->$#* != $second->$#*;
    my $sum = 0;
    $sum+= ($first->[$_]*$second->[$_]) for (0..$first->$#*);
    return $sum;
}

sub vec_prod_f {
    return sprintf("%f", vec_prod($_[0], $_[1]));
}


sub norm {
    my $p = $_[0];
    my $sum = 0;
    $sum+= ($p->[$_])**2 for (0..$p->$#*);
    return $sum;
}

sub norm_f {
    return sprintf("%f", norm($_[0]));
}

sub vec_same {
    my $first = $_[0];
    my $second = $_[1];
    warn "Not the same dimension in vec_same\n" if $first->$#* != $second->$#*;
    for my $s (0..$first->$#*) {
        return undef if $first->[$s] != $second->[$s];
    }
    return 1;
}

sub vec_same_f {
    my $first = $_[0];
    my $second = $_[1];
    warn "Not the same dimension in vec_same_f\n" if $first->$#* != $second->$#*;
    for my $s (0..$first->$#*) {
        return undef if sprintf("%f",$first->[$s]) != sprintf("%f",$second->[$s]);
    }
    return 1;
}

Discussion for the Norm-ONLY Approach

self made

It is possible to calculate all the lengths between points, sort them, and compare whether a cluster of them is equally valued (or whether they are correct multiples of the length of the edges). However, the number of total segments exponentially increases as the dimension increases. And I don't know yet what the minimum number of segment length to be checked is (except for squares).

Another mathematical point is, if we fix a point as "reference origin", we only need to calculate and sort 2^N-1 vectors. Not out of surprise is that the distribution of lengths of the vectors follow the Pascal triangle:

For N = 2, check (1) diagonal;
For N = 3, check (2, 1) diagonals;
For N = 4, check (3, 3, 1) diagonals;
For N = 5, check (4, 6, 4, 1) diagonals;
...

If we calculate all the segments, there are 2^N-1 × (2^N-1) segments, and the distribution of the lengths is a bit more unpleasant to be calculated:

For N = 2, check (2) diagonals;
For N = 3, check (12, 4) diagonals;
For N = 4, check (48, 32, 8) diagonals;
...

Summary

Replication of a square makes a cube; self made

I don't do the &is_5-hypercube. But you can see it will be about checking the orthogonality of the set of 31 vectors origined from one of the vertices, sorting their norms; just bear in mind that the distribution of the lengths of the vectors is (5, 10, 10, 5, 1), check whether the vector sums of the edges are same as diagonals...

Stay alert and healthy! □

Acknowledgement

Thank Simon Proctor for discussion.

Links

I watched them with help of the auto-translated functionality on YouTube.

• La quatrième dimension #1 - Définition - Micmaths
  Discussion of what dimension is through the concept of objects moving parallel to an axis
  (Terminology in Math: a set of pairwise non-parallel vectors spanning space?)
  briefly introduce why we can see only 2D but familiar with (or say, the brain can process) 3D objects
  
  
• La quatrième dimension #2 - Représenter la 4D - Micmaths
  A hypercube appears from 10 min 24 sec to 12 min 48 sec.

Some details on the mathematics of n-hypercubes:

• Wolfram MathWorld: Hypercube

The original image of the tesseract (4-hypercube) is made by Tom Ruen using Stella ‐ a software coded by Robert Webb. The Wikimedia Commons page of the image is here. It is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.

The image of the cube with a face diagonal and a body diagonal marked is made by Ervinpospisil and R. A. Nonenmacher. Its Wikimedia Commons page is here. eleased under CC-BY-SA 4.0/3.0/2.5/2.0/1.0 and GNU Free Documentation License.

Except from images and codes from other personnels (including derived works), the content of this blogpost is released under a copyleft spirit. One may share (full or partial) content of this blogpost on other platform if you share it under the free and open content spirit.

links for CY's full codes: ch-1.pl, ch-2.pl, ch-2-cube-hypercube.pl

Contact on twitter: @e7_87.

Discuss via GitHub issues: here.

Created Date: 28th July, 2021. Last Modified: 1st Aug, 2021.