CY's Seek for Equilibrium (related to TWC 160)
If you want to challenge yourself on programming, especially on Perl and/or Raku, go to https://theweeklychallenge.org, code the latest challenges, submit codes on-time (by GitHub or email).
This is a POST-official-deadline blogpost.
I would like to talk about my solution on the Week 160 Task 2.
As I can remember, that was a busy week for me and I left the task solving late, completed at 11pm (HKT ≡ GMT+8:00) Sunday. While I was writing the code, I noticed a sequence containing zeros will make my algorithm unable to work, and I saw from the official examples, all items are positive integers. Then I made an ASSUMPTION: "This task concerns only positive integers."
During writing the lengthy algorithm, I made a check and found most of the time "the equilibrium index" laying around the middle of the dataset.
I thought, would we need something like binary search? I used some large numbers to test and it seemed that the values were close to the middle of the sequences.
Hence I wrote this algorithm proudly; it starts from the middle index, and moves one step each time:
my $success = $hint_lower == $hint_upper;
return $ind if $success;
while (!$success) {
return -1 if $ind < 1 or $ind > $#n-1;
my $cur_val = $n[$ind];
# Modify the two portions
if ($step == +1) {
$hint_lower = $hint_lower + $n[$expired_ind];
$hint_upper = $hint_upper - $cur_val;
}
elsif ($step == -1) {
$hint_lower = $hint_lower - $cur_val;
$hint_upper = $hint_upper + $n[$expired_ind];
}
# Decide which direction going to move
if ($hint_lower+$cur_val < $hint_upper) {
$new_ind = $ind+1;
}
elsif ($hint_lower > $hint_upper+$cur_val) {
$new_ind = $ind-1;
}
elsif ($hint_lower+$cur_val == $hint_upper) {
$new_ind = $ind+$step; # follow the previous direction
}
elsif ($hint_lower == $hint_upper+$cur_val) {
$new_ind = $ind+$step; # follow the previous direction
}
else {
if ($hint_lower+$cur_val > $hint_upper) {
$new_ind = $ind+1;
}
if ($hint_lower < $hint_upper+$cur_val) {
$new_ind = $ind-1;
}
}
# Prepare for the next loop block, or, stop
$step = $new_ind-$ind;
$success = $hint_lower == $hint_upper;
return $ind if $success;
return -1 if $guessed_step == -$step; # No back and fro!
$guessed_step = $step;
($expired_ind, $ind) = ($ind, $new_ind);
}
On Monday, I compared my solution with teammates'. My solution was the fastest! Then up to some points, I noticed something strange... And I realized the task statement hasn't restricted the numbers to positive integers only. So I misinterpreted a task again.
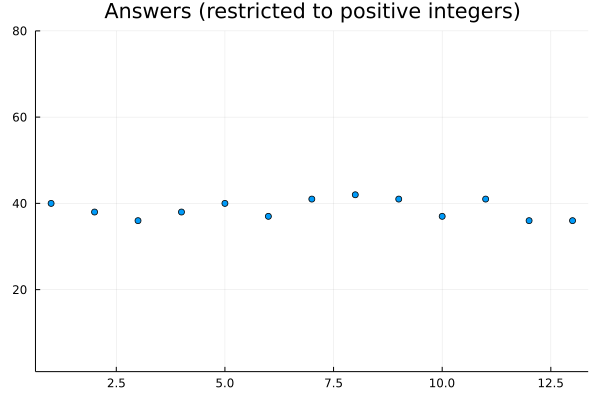
13 points. Data generated by:
for my $case (1..500) { my @n_temp;
$n_temp[$_] = 1 + int rand(40) for (0..79);
my $ans = ei(@n_temp);
next if $ans == -1; say $ans; }
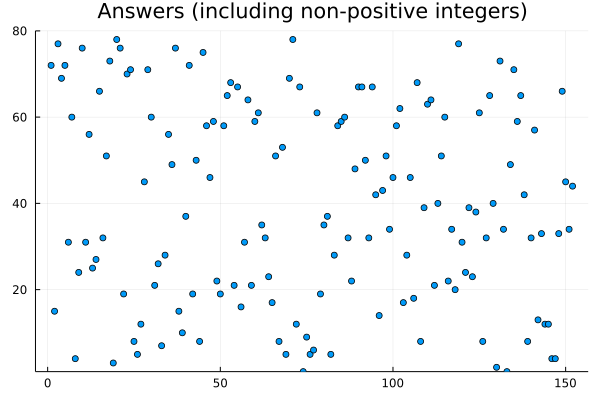
152 points. Data generated by: (cases of more than one equilibrium indices plotted as other cases of a single equilibrium index)
for my $case (1..500) { my @n_temp;
$n_temp[$_] = 20 - int rand(40) for (0..79);
my @as = ei_simple(@n_temp);
next if scalar @as == 0; say join ", ", @as;}
Note: ei() is the subroutine of finding the equilibrium index/indices.
Therefore I submitted a post-deadline solution. At that time I still thought there might be some concentration behavior towards the middle indices. Just now I plotted the above graphs, the second one do not.
A summary for the behavior of "the equilibrium index/indices":
- In the general case, there may be more than one equilirium indices; in a positive-integers-only case, it is either one or none.
- In the general case, the probability of getting an equilirium index is higher.
- In the general case, the equilirium indices, if exist, distribute randomly; in the positive-integers-only cases, they, if exist, concentrate towards the middle index.
link for CY's full code: ch-2.pl (randomized steps), ch-2-wk160-positive.pl
Contact on twitter: @e7_87.
Discuss via GitHub issues: here.
Email: fungcheokyin at gmail.com
Created Date: 19th April, 2022.
Release Date: 28th April, 2022.